2019年9月1日(日)21:00~22:40に開かれました。AtCoder Beginner Contest 139に参加しました。
AtCoder Beginner Contest(ABC)はプログラミングには興味あるけど、何をしていいわからない、そんな人のためのコンテンツです。
問題はAからFまでありだんだんと難しくなっていきます。
今回で5回目の参戦になります。
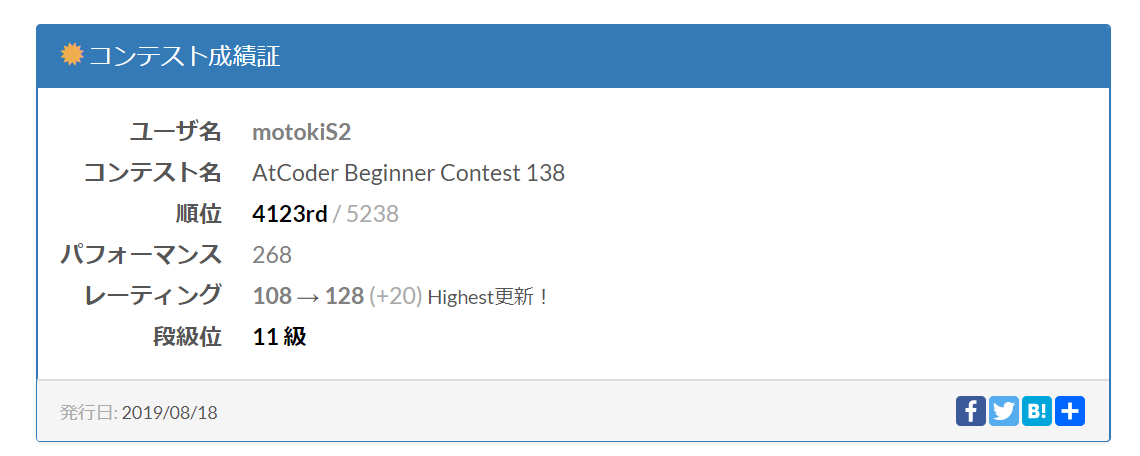
前回のABC138ではCまで完答、Dへの挑戦を相変わらず続けています。
A Tenki
天気予報”S”が実際の天気”T”をどれだけ的中させたかを答える問題です。
入力文字列S,Tを1文字ずつ比較するだけなのですが、
$s = trim(fgets(STDIN));
$t = trim(fgets(STDIN));
$s_sp = str_split($s);
$t_sp = str_split($t);のようにfgetsで入力文字列を受け取った後、文字列を分割して配列に格納するためにstr_splitを使用していました。
なんか2度手間でいい方法ないのかなあってほかの人の解答見ていたら、わざわざstr_splitで分割しなくても$s、$tのままで配列のように添え字をつければ比較できるんですね。。。知りませんでした。
B Power Socket
電源プラグの差込口が1つしかないというなんともいえない高橋君の家でA口のプラグを何個使えばB口にできるかという問題。
A口のプラグを1個増やすと差込口はA増えるだけでなくプラグを使用した分を数えるので合計でA-1個増えます。これがBを超えるまでwhile文で回してみました。わりとスッキリかけていると思います。
<?php
fscanf(STDIN, "%d %d", $a, $b);
$n = 0;
while( $n*($a-1)+1 < $b){
$n++;
}
echo $n;条件文を書く時には難しく考えず、プラグを増やしていった時の差込口の数を単純にまず数えます。
1 → A → 2A-1 のようになっていくので、高校数学的に言うと初項1、公比A-1であるので一般項がN(A-1)+1になるかなって思います。これが差込口の数です。
C Lower
マスと高さの問題、たまに見ますね。
配列の[i]と[i+1]を比較して、[i]>=[i+1]であれば移動OK、カウントを1増やします。[i]<[i+1]となった場合は、今持っているカウントを残しつつも、カウントをリセットし、新たにカウントを増やします。さらにカウントをリセットする際は、残しておいたカウントと今持っているカウントどちらが大きいか比べて大きいほうを残します。
<?php
fscanf(STDIN, "%d", $n);
$h = explode(" ",fgets(STDIN));
$h = array_map("intval", $h);
$move = 0;
$moveMax = 0;
for($i=0; $i<$n-1; $i++) {
if($h[$i] >= $h[$i+1]) {
$move++;
} else {
$moveMax = max($move, $moveMax);
$move = 0;
}
}
echo max($move, $moveMax);$moveが現在のカウント、$moveMaxが、保持している最大のカウントです。
ちなみに最後のecho文でmax関数を使わずに$moveMaxだけを出力しようとすると、最後のmoveが一番大きかった場合にこれが出力できません。
これがわからなかったせいで苦戦してました。
D ModSum
なんかもしかしてこれでいいのか。。。?と提出したらACできた初D問題。
Nはかならず商と余りが出るのに対して1からN-1までの数字は商を0にあとはあまりにすることができることに気付けるかどうかだと思います。
商を0にするには割る数より割られる数を小さくすればOK
具体的に言うと2÷3は0あまり2、4÷9は0あまり4、あまりの合計を最大化したいので商は0でいたほうがいいはず
さらにいうと割る数と割られる数は同じ数だけ用意してもらっているので割られる数Mに対して割る数M+1を用意すればOK
で余った割る数1は商を0にできないNに充てておけばいいかなと
つまり1~N-1の和を出せばそれが答えになると思います。
<?php
fscanf(STDIN, "%d", $n);
$ans = ($n*($n-1))/2;
echo $ans;Dとは思えないほどのスッキリ差ですね。
これ最初for文で足し合わせていたのですがTLEになってしまったので、またしても高校数学で習った1~Nまでの合計(今回はN-1までですが)を使ったところ無事AC
今回の成績
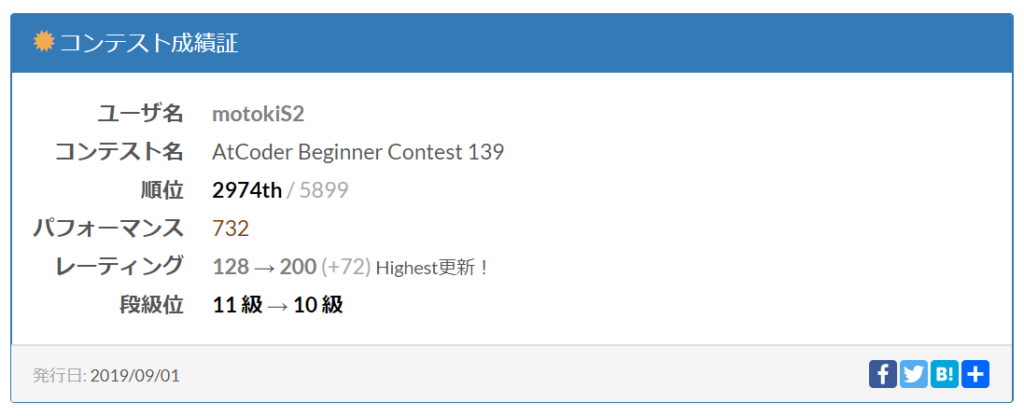
10級に上がりましたね。
なんかもっとぐっと上がるためにはD,Eをコンスタントにクリアし続ける必要があるのかな、と感じました。今回はDが簡単だったこともあるので。
Eの問題はちょっとみたのですが、なんか難しそうなのでパスしてしまいました。こういうのやっていかないと実力つかないんですけどね(笑)
次回の140は私用により参加できないので個人的に取り組むことにします。
ではまた

コメント