この記事ではバックプロパゲーションによってどのように出力層から入力層へ誤差が伝播していくのか簡単な式を用いて説明していくものです。コード等は一切なしで説明していきます。
バックプロパゲーション(誤差逆伝播法)はニューラルネットワークのトレーニングを非常に効率よく行うアルゴリズムであり、出力と正解の誤差がネットワークを逆伝播することにより、ネットワークの重みとバイアスを最適化します。
参考書に乗っているバックプロパゲーションの式は個人的にとても難しく感じますが、実装されているコードを使えばとりあえず使えてしまう。そんなイメージです。
しかし伝播をよく見ることで、重みやバイアスを変化させたときのニューラルネットワーク全体の挙動の変化に関して深い洞察が得られるのでぜひとも理解しておきたい部分です。
参考書籍及びURLは
[第2版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践
主にこれらを使用して説明していきます。式の大部分は上の書籍です。
使用する関数
コスト関数
$$
J\left(\bf{w}\right) = – \left[\sum_{i=1}^ny^{[i]}log\left(a^{[i]}\right) + \left(1 – y^{[i]}\right)log\left(1 – a^{[i]}\right)\right]
$$
$a^{[i]}$はシグモイド関数
$$
a^{[i]} = \phi\left(z^{[i]}\right) = \frac{1}{1 + e^{-z^{[i]}}}
$$
L2正則化項 (バイアスユニットは正則化しない
$$
L2 = \lambda\left|\bf{w}\right|_2^2 = \lambda\sum_{j=1}^mw_j^2
$$
L2正則化項を加えたコスト関数
$$
J\left(\bf{w}\right) = – \left[ \sum_{i=1}^ny^{[i]}log\left(a^{[i]}\right) + \left(1 – y^{[i]}\right)log\left(1 – a^{[i]}\right) \right] + \frac{\lambda}{2}\left|\bf{w}\right|_2^2
$$
書籍では他クラス分類の多層パーセプトロンを実装し、t個の要素からなる出力ベクトルが返されます。
MNISTの例では手書き数字[0,1,2,3,4,5,6,7,8,9]の10クラス判別を行うのでt=10です。
ネットワーク全ての活性化ユニットtに対してコスト関数を一般化し、入力データiに対する各クラスjの誤差をコストに加えます。
$$
J\left(\bf{w}\right) = – \left[ \sum_{i=1}^n\sum_{j=1}^{t}y^{[i]}_{j}log\left(a^{[i]}_{j}\right) + \left(1 – y^{[i]}_{j}\right)log\left(1 – a^{[i]}_{j}\right)\right]
$$
さらに一般化された正則化項は、各層の重みをそれぞれ足し合わせたもの(重みがある層の数×入力ユニット×出力ユニット)
$$
J\left(\bf{w}\right) = – \left[ \sum_{i=1}^n\sum_{j=1}^{t}y^{[i]}_{j}log\left(a^{[i]}_{j}\right) + \left(1 – y^{[i]}_{j}\right)log\left(1 – a^{[i]}_{j}\right)\right] + \frac{\lambda}{2}\sum_{l=1}^{L-1}\sum_{i=1}^{u_{l}}\sum_{j=1}^{u_{l+1}}\left(w_{j,i}^{(l)}\right)^2
$$
目的はこのコスト関数$J(W)$を最小化することであり、すべての層の重みごとに行列$W$の偏微分係数を計算する必要があります。
バックプロパゲーションの前に
バックプロパゲーションを行う際には、出力から入力に向かって逆伝播していくため、まずはフォワードプロパゲーションを適用する必要があります。この式の説明はここでは行わないですが、バックプロパゲーションで躓いたって人であればおそらくフォワードプロパゲーションの理解まではできていることでしょう。
$Z^{(h)} = A^{(in)}W^{(h)}$ (隠れ層の総入力)
$A^{(h)} = \phi\left(Z^{(h)}\right)$ (隠れ層の活性化関数)
$Z^{(out)} = A^{(h)}W^{(out)}$ (出力層の総入力)
$A^{(out)} = \phi\left(Z^{(out)}\right)$ (隠れ層の活性化関数)
シンプルなニューラルネットワーク
バックプロパゲーションの式の流れだけを掴むためにニューラルネットワークをとてつもなくシンプルなものにします。こちらです
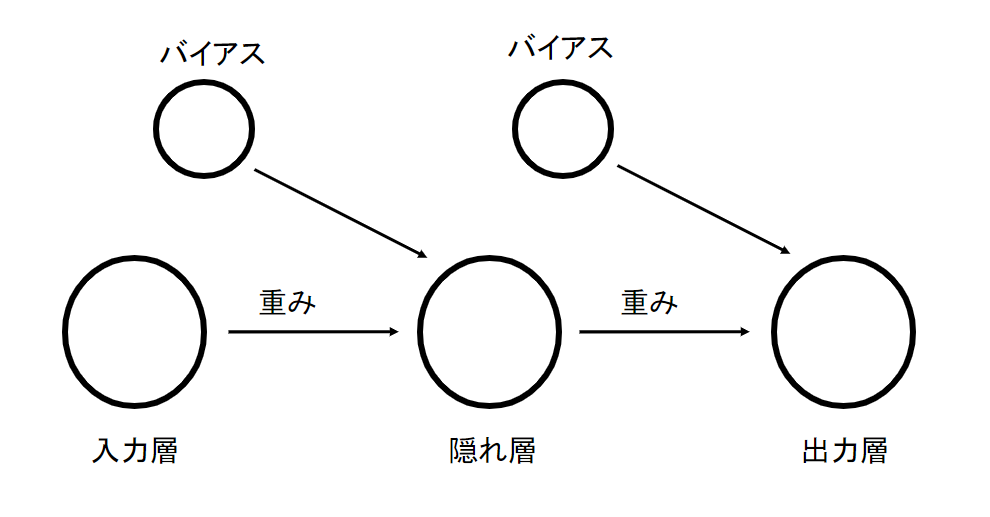
入力層-隠れ層-出力層からなるそれぞれのユニットが1つのみのニューラルネットワークを考えてみます。この形でニューラルネットに含まれる行列を無視して計算できるようにします。最終的な結果はユニットが複数のものと同じになるはずなので安心してください。
連鎖律の概念(合成関数の微分)
バックプロパゲーションを行うにあたって必ず使うものです。高校数学で言う合成関数の微分と言うと個人的にしっくりきます。
$$
\frac{d}{dx}\left[f(g(x))\right] = \frac{df}{dg}\cdot\frac{dg}{dx}
$$
任意の長さの関数を合成するための連鎖律を利用できます。
$$
\frac{dF}{dx} = \frac{d}{dx}f(g(h(u(v(x))))) = \frac{df}{dg}\cdot\frac{dg}{dh}\cdot\frac{dh}{du}\cdot\frac{du}{dv}\cdot\frac{dv}{dx}
$$
繋げすぎて若干ギャグみたいな形になっていますが、実際にここまで長くなることもあります。
バックプロパゲーションの導出
前置きが長くなりましたが、いよいよ式の流れを見ていきます。求める最終的な形を記載しておきます。
出力層の誤差
$$
\boldsymbol{\delta}^{(out)} = \boldsymbol{a}^{(out)} – \boldsymbol{y}
$$
隠れ層の誤差
$$
\boldsymbol{\delta}^{(h)} = \boldsymbol{\delta}^{(out)}\left(W^{(out)}\right)^T \odot \frac{\partial\phi\left(\boldsymbol{z}^{(h)}\right)}{\partial\boldsymbol{z}^{(h)}} \
\odot はアダマール積(要素ごとの積)\
$$
$$
\frac{\partial\phi\left(z^{(h)}\right)}{\partial z^{(h)}} = \left(\boldsymbol{a}^{(h)}\odot\left(1-\boldsymbol{a}^\left(h\right)\right)\right)
$$
これらの誤差項を用いてコスト関数の偏微分計算を次のように記述します。
$$
\frac{\partial}{\partial w_{i,j}^{(out)}}J(W) = a_{j}^{(h)}\delta_{i}^{(out)} \
$$
$$
\frac{\partial}{\partial w_{i,j}^{(h)}}J(W) = a_{j}^{(in)}\delta_{i}^{(h)} \
$$
今回は上で説明したようにシンプルなニューラルネットワークを使用するので添え字を整理すると
$$
\begin{align}
&z^{(h)} = a^{(in)}w^{(h)} + b^{(h)} \\
&a^{(h)} = \frac{1}{1 + exp^{-z^{(h)}}} \\
&z^{(out)} = a^{(h)}w^{(out)} + b^{(out)} \\
&a^{(out)} = \frac{1}{1 + exp^{-z^{(out)}}}
\end{align}
$$
$$
J\left(w\right) = – \left(ylog\left(a^{(out)}\right) + \left(1 – y\right)log\left(1 – a^{(out)}\right)\right)
$$
$w^{(out)}$で微分
$$
\begin{align*}
a^{(out)} = \phi(z^{(out)}) = \phi(a^{(h)}w^{(out)} + b^{(out)}) \\
\frac{\partial J(w)}{\partial w^{(out)}} = \frac{\partial J(w)}{\partial a^{(out)}}\cdot \frac{\partial a^{(out)}}{\partial z^{(out)}}\cdot \frac{\partial z^{(out)}}{\partial w^{(out)}} \\
\end{align*}
$$
$J(w)$は$a^{(out)}$の関数で、$a^{(out)}$は$z^{(out)}$の関数で、$z^{(out)}$は$w^{(out)}$の関数です。微分する変数と関係ない変数は定数として扱うことに注意ください。
それぞれの微分した形は以下の通りです。
$$
\begin{align*}
&\frac{\partial J(w)}{\partial a^{(out)}} = – \frac{y – a^{(out)}}{a^{(out)}(1-a^{(out)})} \\
&\frac{\partial a^{(out)}}{\partial z^{(out)}} = a^{(out)}(1 – a^{(out)}) \\
&\frac{\partial z^{(out)}}{\partial w^{(out)}} = a^{(h)} \\
\end{align*}
$$
つまりこれらをかけ合わせればよいので(連鎖律)
$$
\begin{align*}
&\frac{\partial J(w)}{\partial w^{(out)}} = – \frac{y – a^{(out)}}{a^{(out)}(1-a^{(out)})} a^{(out)}(1 – a^{(out)}) a^{(h)} \\
&= (a^{(out)} – y)a^{(h)} \\
&\delta^{(out)} = a^{(out)} – y \\
&\frac{\partial J(w)}{\partial w^{(out)}} = a^{(h)}\delta^{(out)} \\
\end{align*}
$$
このようにして隠れ層の出力×何かの形にできます。この何かの部分がいわゆる誤差項と呼ばれるものになっています。
自分が初めてバックプロパゲーションの学習を行った時、誤差項というものは出力層の値と正解ラベルの誤差から導き出せるものなのだ、と思いました。結果的にそれは間違いではなかったのですが、そうなるようにコスト関数を設定しているため、という認識がありませんでした。なので単に正解と出力の差が誤差項である!と思っていると「では隠れ層の誤差項は隠れ層の出力と、何の差で導き出せるのか?」とイメージが急にしずらくなる問題が発生すると思います。
$w^{(h)}$で微分
では同様に$w^{(h)}$でも微分していきたいと思います。
$$
\begin{align}
&a^{(out)} = \phi(z^{(out)}) = \phi(a^{(h)}w^{(out)} + b^{(out)}) \\
&a^{(h)} = \phi(z^{(h)}) = \phi(a^{(in)}w^{(h)} + b^{(h)}) \\
\end{align}
$$
今回も連鎖律を使用して微分していきます。特に気を付けてほしいところは今回は$w^{(h)}$での微分であるため$w^{(out)}$及びその関数は定数として扱うということです。
$$
\begin{align}
&\frac{\partial J(w)}{\partial w^{(h)}} = \frac{\partial J(w)}{\partial a^{(out)}}\cdot \frac{\partial a^{(out)}}{\partial z^{(out)}}\cdot \frac{\partial z^{(out)}}{\partial a^{(h)}} \cdot \frac{\partial a^{(h)}}{\partial z^{(h)}}\cdot \frac{\partial z^{(h)}}{\partial w^{(h)}}\\
&\frac{\partial J(w)}{\partial a^{(out)}}\cdot \frac{\partial a^{(out)}}{\partial z^{(out)}} = \delta^{(out)} \\
\end{align}
$$
ここで先ほど$w^{(out)}$で微分した際に出てきた形と同じものがでてきたのでその結果を使います。
$$
\begin{align}
&\frac{\partial z^{(out)}}{\partial a^{(h)}} = w^{(out)}\\
&\frac{\partial a^{(h)}}{\partial z^{(h)}} = a^{(h)}(1 – a^{(h)})\\
&\frac{\partial z^{(h)}}{\partial w^{(h)}} = a^{(in)} \\
&\delta^{(h)} = \delta^{(out)}w^{(out)}a^{(h)}(1 – a^{(h)}) \\
&\frac{\partial J(w)}{\partial w^{(h)}} = a^{(in)}\delta^{(h)} \\
\end{align}
$$
最終的に入力層の出力×何かの形になります。そして先ほど同様この何かこそが隠れ層の誤差項になるのです。これで簡単ではありますが、バックプロパゲーション誤差項の導出が完了しました。
導出からもわかるバックプロパゲーションのすごさ
ここで気づく方もいると思いますが、今$w^{(out)}$と$w^{(h)}$でそれぞれ$J(w)$の微分を行いました。しかし、連鎖律の結果をうまく使うことで、実際に計算した量はほぼ同じ量だったのではないでしょうか。隠れ層からの重みで微分した場合と、入力層からの重みで微分した場合、出力から遠い入力層の重みで微分した場合のほうが量が多くより複雑な計算になることが想像されます。しかしそうならないように式ができています。
これこそがバックプロパゲーションがニューラルネットワークの重みの学習で使われる理由です。途中までの微分した結果が最後の枝分かれまで同じものを使用できるからです。
今回はユニット数が1つだったのでそこまで実感がわかなかったかもしれませんが、例えば入力ユニットが2つだったことを考えると出力から隠れ層までの微分した結果をその2つに同じ結果を使うことができます。
この記事で少しでもバックプロパゲーションの理解が進む方がいれば幸いです。



コメント